Simple Linear Regression using Neural Network

To understand how a Deep Neural Network works, you need to play around with smaller models of Neural Network. Every linear model can be represented as a neural network with no hidden layer. We will see how a simple linear regression looks like through the lens of a deep neural network (not deep, but a shallow :D). In other articles we will do it for a logistic regression, and other linear models.

Simple Linear Regression

You have $n$ data points $(x_i, y_i) \mid _{i = 1}^n$ corresponding to the variables $(X,Y)$. A simple linear regression is a model whose functional form is $Y = wX + b$, if we eliminate the probabilistic assumption. Understand that the probabilistic assumption helps us to model the behaviour of the algorithm for future data point. In other words, the probabilistic assumption give an idea of the data generation process.

Understanding a Neural Network for Simple Linear Regression

Let's try to design a neural network for a simple linear regression. As you can see, there is only input of only one data feature $X$, and it needs no hidden layer. We need a linear activation function $\sigma(z) = z$ to keep the output same from the previous node. Then, we use the square loss function to model the loss function for a single data point. We repeat this for multiple data points, and minimise the macro loss function formed by adding the micro loss functions.

Coding a Neural Network for Simple Linear Regression

We will code in python with the following steps. Let me help you understand the code properly. We use simulated data to show an example.

Step 1: Simulate a Linear Model Dataset

import numpy as np
import pandas as pd

# Generate random data for a linear model
np.random.seed(0)
X = np.random.rand(100, 1)  # Input feature
y = 2 * X + 1 + 0.1 * np.random.randn(100, 1)  # Output feature with some noise

# Create a DataFrame
data = pd.DataFrame({'X': X.flatten(), 'y': y.flatten()})

# Display the first few rows of the dataset
print(data.head())

Step 2: Fit Linear Regression using a Neural Network with PyTorch

import torch
import torch.nn as nn
import torch.optim as optim

# Convert pandas DataFrames to PyTorch tensors
X_tensor = torch.tensor(X, dtype=torch.float32)
y_tensor = torch.tensor(y, dtype=torch.float32)

# Define a simple linear regression model
class LinearRegressionModel(nn.Module):
    def __init__(self, input_dim):
        super(LinearRegressionModel, self).__init__()
        self.linear = nn.Linear(input_dim, 1)  # One output unit

    def forward(self, x):
        return self.linear(x)

# Instantiate the model
input_dim = 1  # Since we have one input feature
model = LinearRegressionModel(input_dim)

# Define the loss function (Mean Squared Error) and optimizer (Stochastic Gradient Descent)
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)

# Training loop
num_epochs = 1000
for epoch in range(num_epochs):
    # Forward pass
    outputs = model(X_tensor)
    loss = criterion(outputs, y_tensor)

    # Backpropagation and optimization
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    if (epoch + 1) % 100 == 0:
        print(f'Epoch [{epoch + 1}/{num_epochs}], Loss: {loss.item():.4f}')

# Get the learned weights and bias
learned_weights = model.linear.weight.item()
learned_bias = model.linear.bias.item()

print(f'Learned weight: {learned_weights:.4f}, Learned bias: {learned_bias:.4f}')

Step 3: Plotting the Loss Function over Epochs

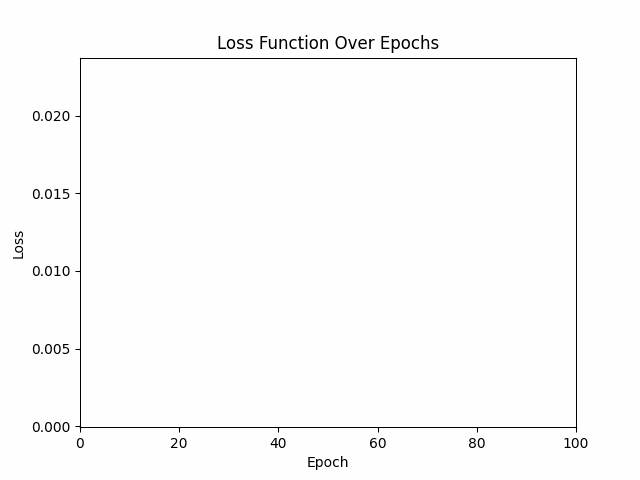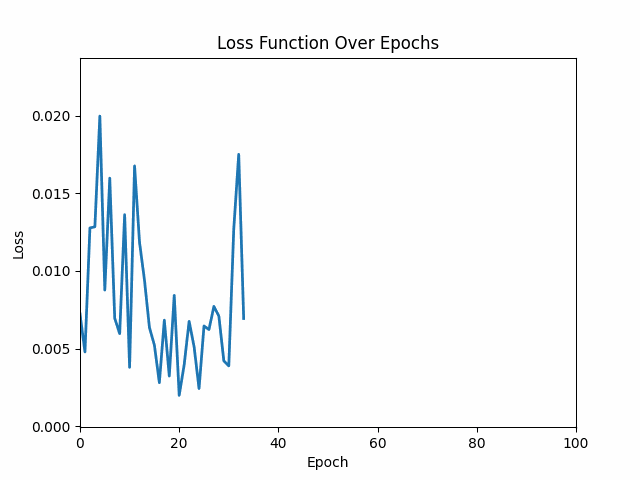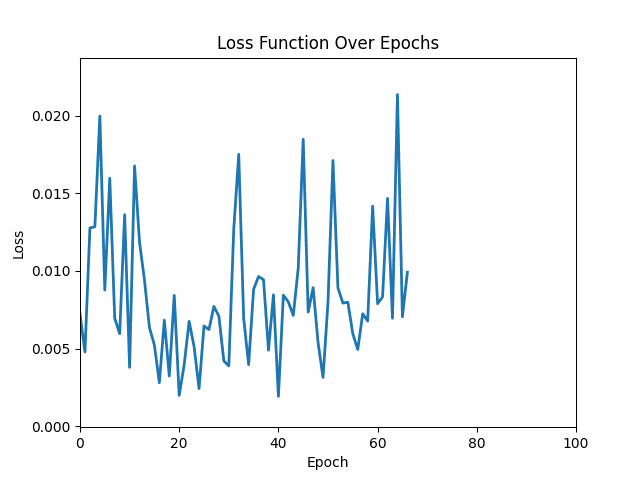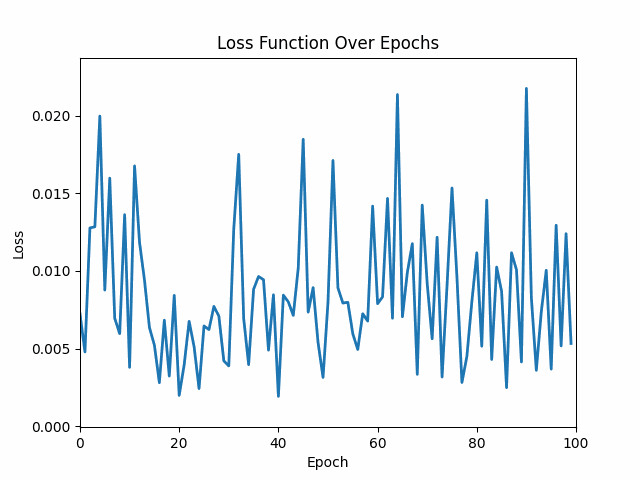
In the upcoming articles, we will discuss what each line of code in building a neural network is important, and how exactly does it work. This is important to understand from building a neural network point of view.

Learn. Code. Apply.

Statistics. Machine Learning.

Simple Linear Regression using Neural Network