Introduction to MLE
You have a coin. You are interested to know the probability of getting heads with your coin. You toss your coin 8 times. You get the following sequence. H, H, T, H, T, T, H, H
How do you find an optimum value for the probability of heads? One rational to obtain is just taking the average number of heads, that you have got that is $\frac{5}{8}$. Is that reasonable? If yes, why?
Let me give you another example, which involves a bit more probability.
You ask your friend to select a secret $\mu$ and ask it to generate a sample of 100 random numbers from N$(\mu, 1)$, and give it to you.
You draw its histogram. You want to find out which $\mu$ is reasonable. So, you try to overlay the different density functions on the top of the histogram for certain values of $\mu$ and take a rational guess. Here is what you have got.
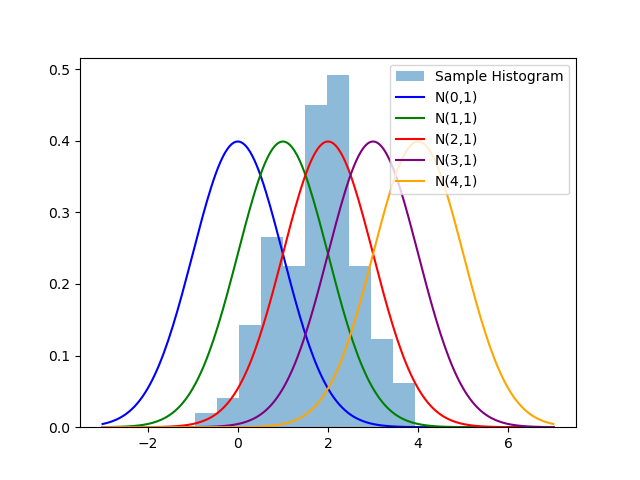
Naturally, you see that $2$ is the best guess among your options. Is there a better guess? How to make it formal?
This is the question that is answered by the Maximum Likelihood Estimation procedure.
Understanding the algorithm of MLE
Let's take the example of the coin, above. We need to start using our formal knowledge of probability now.
We have a sample of eight heads and tails. We can model the process as a sequence of Bernoulli trials with success probability $p$, where success happens if you get heads. We write it formally as
$X_1, X_2, \cdots, X_8 \sim$ i.i.d. Ber$(p)$.
We have got the realizations as $1, 1, 0, 1, 0, 0, 1, 1$. Now, let's fix a probability $p= \frac{1}{3}$. For this probability, let's find out the probability of actually observing this sample from the given distribution. Let's denote it as $L(\frac{1}{3})$.
$$L(\frac{1}{3}) = \binom{8}{5} (\frac{1}{3})^5 \cdot (\frac{2}{3})^3 \sim 0.0683$$
Now, we will calculate this for various values of $p$ instead of just $\frac{1}{3}$.
| ( p ) | Probability of 5 heads out of 8 tosses |
|---|---|
| 0.3 | 0.0461 |
| 0.4 | 0.1239 |
| 0.5 | 0.2188 |
| 0.6 | 0.2783 |
| 0.7 | 0.2541 |
| 0.8 | 0.1463 |
| 0.9 | 0.0331 |
As you can see the probability values are different for different values of $p$. You can see that for $p = 0.6$, it reaches the maximum among the values, and then decreases on both sides.
So a natural question is the following. What does it mean to have a high probability of 5 heads and a low probability of 5 heads for different values of $p$?
If you think carefully, you will find out that a high probability of heads with a specific value of $p$ means that for that value of $p$, the chance of observing the observed sample is high. For example, as you can see as the heads are around 5 out of 8, the chance of observing the sample from a coin with less chance of success of heads is small, and for extremely high chances of getting heads is also small.
Woohoo! This means that for a specific value of $p$, the probability value of getting 5 heads is a very good measure of the fact that the sample resonates with that corresponding value of $p$. The lower the probability value of getting 5 heads, the lower the conherence of the sample we have observed and the unknown $p$ value, we want to know. The higher the probability of getting 5 heads, the higher the coherence.
Let's try to understand this mathematically.
Probability of 5 heads out of 8 := $L(p) = \binom{8}{5} \cdot p^5 \cdot (1-p)^3 $.
Great, this is a function of $p$. This means using calculus we can find for which value of $p$, this is going to be the maximum, and voila, that's exactly what we are looking for.
Finding the best value of unknown $p$, for which the sample actually resonates, and is coherent from the underlying unknown process, which we want to know.
Observe that $\binom{8}{5}$ is not important for finding the best value of $p$, because it is just a constant as it doesn't contain $p$. Without that constant, let's plot the function curve $ p^5 \cdot (1-p)^3$.
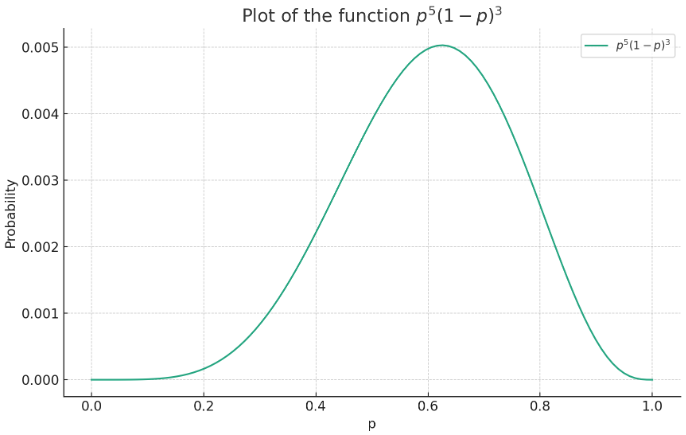
As you can see around 0.6 something value of $p$, the probability of getting 5 heads achieves the maximum.
Can we find that value analytically? Yes, of course. Let's do some calculus.
$$\frac{dL(p)}{dp} \left( p^5 (1-p)^3 \right) = -3p^5(1 - p)^2 + 5p^4(1 - p)^3$$
Equating $\frac{dL(p)}{dp} = 0$, we get $p = \frac{5}{8} = 0.625$. Woo! Woo!
That's interesting! That's exactly what we have guessed. This seems to be working in accordance with our intuition, right? This is called the maximum likelihood estimation process.
This needs to be formalized more for applying this to a vast variety of problems.
In another post, I will be formalizing the mathematics, and the probability behind the maximum likelihood estimation process.
